数学之路-数据分析进阶-广义线性模型，数据分析进阶

文章由LinuxBoy分享于2019-03-27 06:03:44热评（514）

在统计学上，广义线性模型 (Generalized linear model) 是一种受到广泛应用的线性回归模式。此模式假设实验者所量测的随机变量的分布函数与实验中系统性效应(即非随机的效应)可经由一链结函数(link function)建立起可资解释其相关性的函数。

广义线性模型（generalized linear model, GLM)是简单最小二乘回归（OLS)的扩展,在广义线性模式中，假设每个资料的观测值 $\mathbf Y$ 来自某个指数族分布。该分布的平均数 $\boldsymbol\mu$ 可由与该点独立的X解释：

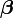\operatorname{E}(\boldsymbol{y}) = \boldsymbol{\mu} = g^{-1}(\mathbf{X}\boldsymbol{\beta})

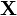其中 $E(\boldsymbol y)$ 为 $\boldsymbol y$ 的期望值， $\mathbf X\boldsymbol\beta$ 是由未知待估计参数 $\boldsymbol\beta$ 与已知变量 $\mathbf X$ 构成的线性估计式， $g$ 则为链结函数。

在此模式下， $\boldsymbol y$ 的方差 $V$ 可表示为：

\operatorname{Var}(\boldsymbol{y}) = \operatorname{V}( \boldsymbol{\mu} ) = \operatorname{V}(g^{-1}(\mathbf{X}\boldsymbol{\beta})).

一般假设 $V$ 可视为一指数族随机变量的函数。

未知参数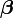 $\boldsymbol\beta$ 通常会以最大概似估计量, 殆最大概似估计量, 或以贝氏方法来估计。

链结函数解释了线性预测子与分布期望值的关系。链结函数的选择可视情形而定。通常只要符合链结函数的值域有包含分布期望值的条件即可。

当使用具正则参数θ的分布时，链结函数需符合X^TY 为β的充份统计量此一条件。这在θ与线性预测子的链结函数值相等时方成立。下面列出若干指数族分布的典则链结函数及其反函数(有时称为均值函数)：

典则链结函数
分布	名称	链结函数	均值函数
正态	恒等	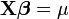$\mathbf{X}\boldsymbol{\beta}=\mu\,\!$	$\mu=\mathbf{X}\boldsymbol{\beta}\,\!$
指数	倒数	$\mathbf{X}\boldsymbol{\beta}=\mu^{-1}\,\!$	$\mu=(\mathbf{X}\boldsymbol{\beta})^{-1}\,\!$
Gamma	倒数	$\mathbf{X}\boldsymbol{\beta}=\mu^{-1}\,\!$	$\mu=(\mathbf{X}\boldsymbol{\beta})^{-1}\,\!$
逆高斯	二次倒数	$\mathbf{X}\boldsymbol{\beta}=\mu^{-2}\,\!$	$\mu=(\mathbf{X}\boldsymbol{\beta})^{-1/2}\,\!$
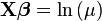泊松	自然对数	$\mathbf{X}\boldsymbol{\beta}=\ln{(\mu)}\,\!$	$\mu=\exp{(\mathbf{X}\boldsymbol{\beta})}\,\!$
二项式	Logit	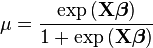$\mathbf{X}\boldsymbol{\beta}=\ln{\left(\frac{\mu}{1-\mu}\right)}\,\!$	$\mu=\frac{\exp{(\mathbf{X}\boldsymbol{\beta})}}{1 + \exp{(\mathbf{X}\boldsymbol{\beta})}}\,\!$
多项式	Logit